Here are the math answers to our example test.
Please read each explanation carefully, paying special attention to the illustrations.
You can get further math help in our free study guide.
Math Answers (1)
What is the value of x − 3/2 − x when x = 1?
The correct answer is: B
Substitue 1 for x.
(1 − 3) ÷ (2 − 1) =
−2 ÷ 1 =
−2
Math Answers (2)
A runner of a 100 mile endurance race ran at a speed of 5 miles per hour for the first 80 miles of the race and x miles per hour for the last 20 miles of the race. What equation represents the runner's average speed for the entire race?
The correct answer is: A
Divide the number of miles by the miles per hour to get the time for each part of the race.
So, for the first part of the race, the hours are calulated as follows:
80 ÷ 5
For the second part of the race, we take the remaining mileage and divide by the unknown variable:
20 ÷ x
The total amount of miles for the race is then divided by the total hours to get the average miles per hour for the entire race. Since the entire race is 100 miles, the solution is as follows:
100 ÷ [(80 ÷ 5) + (20 ÷ x)]
Math Answers (3)
What is the determinant of the following matrix?
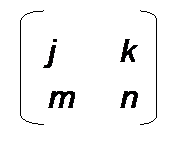
The correct answer is: C
In order to find the determinant for a two-by-two matrix, you need to cross multiply and then subtract.
So j is multiplied by n and m is multiplied by k.
Then we subtract the two terms to get the determinant.
jn − mk
Math Answers (4)
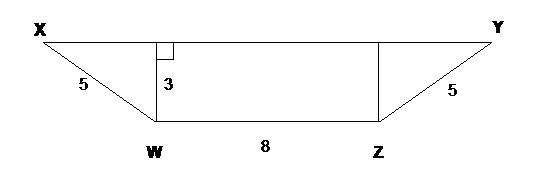
In the above figure, XY and WZ are parallel, and lengths are provided in units. What is the area of trapezoid WXYZ in square units?
The correct answer is: D
First, calculate the area of the central rectangle. Remember that the area of a rectangle is length times height.
8 × 3 = 24
Using the Pythagorean theorem, we know that the base of each triangle is 4.
52 = 32 + base2
25 = 9 + base2
25 − 9 = 9 − 9 + base2
16 = base2
4 = base
Then calculate the area of each of the triangles on each side of the central rectangle. Remember that the area of a triangle is base times height divided by 2.
(4 × 3) ÷ 2 = 6
So the total area is the area of the main rectangle plus the area of each of the two triangles.
24 + 6 + 6 = 36
Math Answers (5)
The street that runs between the hospital (H) and the police station (P) in the illustration below forms a 65° angle. If the police station (P) is 2.5 miles from the fire station (F), what equation below calculates the distance of the fire station from the hospital?
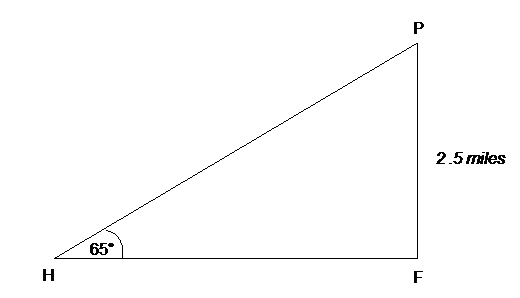
The correct answer is: B
Here trigonometric formulas for calulating the sine, cosine and tangent of any given angle A, as shown in the illustration below.
sin A = x/z
cos A = y/z
tan A = x/y
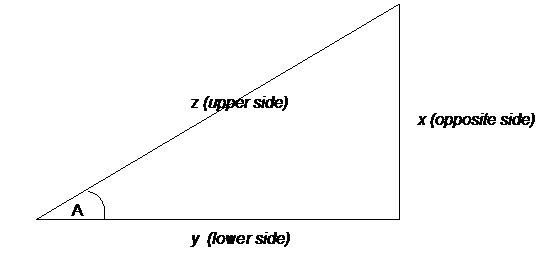
In other words, for any angle, sine is calculated by taking the measurement of the opposite side divided by the measurement of the upper side of the triangle.
Cosine is calculated by taking the measurement of the lower side divided by the measurement of the upper side of the triangle.
Tangent is calculated by taking the measurement of the opposite side divided by the measurement of the lower side of the triangle.
We know the distance from the fire station to the police station is 2.5 miles. The line connecting these points (FP) forms the opposite side of the triangle HFP.
We need to calculate the distance between the hospital and the fire station. The line connecting these points (HF) forms the lower side of the triangle.
Since we have the opposite side and the lower side, we need to use the formula above for the tangent of an angle.
So the length from the hospital to the fire station is calculated by taking the tangent of the angle commencing at the hospital, in this case the tangent of 65°.
tan 65° = FP ÷ HF
Divide each side of the equation by tan 65° and substitute 2.5 miles for FP in order to isolate the unknown variables.
tan 65°÷ tan 65°= 2.5 ÷ HF ÷ tan 65°
1 = 2.5 ÷ HF ÷ tan 65°
Now multiply each side of the equation by HF in order to isolate the unknown variables.
1 × HF = 2.5 ÷ (HF × HF) ÷ tan 65°
HF = 2.5 ÷ tan 65°
