The trigonometry section of the Compass will have calculations on these types of trigonometric concepts.
www.compass-test-practice.com
The trigonometry section of the Compass will have calculations on these types of trigonometric concepts.
Trigonometric equations include the calculation of sine, cosine, and tangent.
Problem: If cos A = y/z and tan A = x/y, then sin A = ?
Solution: The correct answer is sin A = x/z.
For these types of questions, you have to memorize the trigonometric relationships below, which are always valid for any given angle.
sin A = x/z
cos A = y/z
tan A = x/y
For an illustration of these basic trigonometry concepts with further explanations, please click here.
Then have a look at the diagram at the bottom of that page.
Right-angle trigonometry will cover the calculation of sine, cosine, and tangent for trigonometric figures that contain ninety degree angles.
Problem: In the right angle in the figure below, angle Z is 50 degrees.
The length of XZ is 5 units.
sin 50° = 0.766, cos 50° = 0.643, and tan 50° = 1.192.
Approximately how many units long is XY?
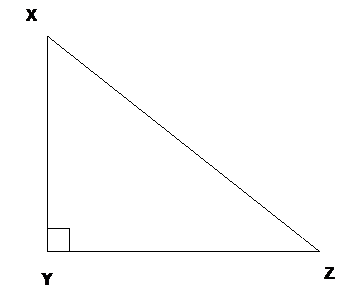
Solution: The sine of angle Z is calculated by dividing XY by XZ.
sin Z = XY/XZ
sin Z = XY/5
Since angle Z is 50 degrees, we can substitute values as follows:
sin Z = XY/5
0.766 = XY/5
0.766 × 5 = XY/5 × 5
0.766 × 5 = XY
3.83 = XY
The math test will have trigonometric calculations of angles that are multiples of thirty or forty-five degrees.
Problem: ∠XYZ is an isosceles triangle, where XY is equal to YZ.
Angle Y is 60° and points W, X, and Z are co-linear.
What is the measurement of ∠WXY?

Solution: We know that any straight line is 180.
So, we need to subtract the degree of the angle stated in the problem (∠XYZ) from 180°.
180° − 60° = 120°
There are two remaining angles lying on the straight line.
One is ∠WXY, and we will call the other one that extends past point Z ∠YZV.
The sum of these two remaining angles, ∠WXY and ∠YZV equals 120°.
Since ∠XYZ is isosceles, the remaining angles will be equal to each other since their two sides, XY and YZ are equal.
So, we divide the remaining degrees by two in order to find out how many degrees there are in ∠WXY and ∠YZV.
120°÷ 2 = 60°
In these types of problems you will see sin, cos, tan, or cot with the > or < signs.
A function on this part of the examination will be in the form of F(x) < 0 or F(x) > 0, in which F(x) contains a trigonometric function.
You will also be asked questions about radians and arcs.
Problem: An arc length of θ on a circle of radius one subtends an angle of how many radians at the center of the circle?
Solution: The radian measure of a central angle of a circle is defined as the ratio of the length of the arc the angle subtends, divided by the radius of the circle.
When working with a circle with radius 1, the length of the arc equals the radian.
Or stated conversely, the radians will be equal to the arc length.
So the correct answer is θ.
For practical trigonometric problems you will need to know how to calculate the distance between two points.
These points might lie on a street or road connecting two locations.
For a practical trigonometry problem, please go to the math sample test.
If you had difficulties with the exercises on these pages, you may need more math help.