Geometry

The geometry section of the Compass includes calculations on each of the types of geometric shapes and figures mentioned below.

Have a look at the question types in each section. Then try to do the problems and study the solutions.

How to Get Our Math Download

Geometry - Calculation of Angles

You will need to calculate angles on the geometry part of the Compass test.

Please have a look at the problems below/.

Problem:

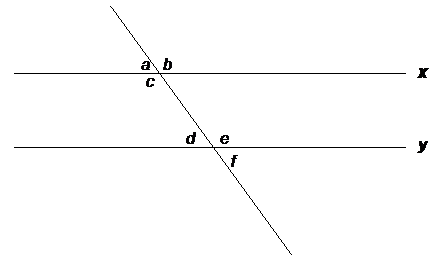
In the figure above, x and y are parallel lines, and the diagonal line is a transversal crossing both x and y.

Which of the three angles are equal in measure?

So, for example, angles a and d are equal, and angles b and e are equal.

Also remember that opposite angles will be equal when bisected by two parallel lines, such as lines x and y in this problem.

Angles b and c are opposite, and angles d and f are also opposite.

So the three angles a, d, and f are equal.

In addition, the three angles b, c, and e are equal.

Geometry - Triangles

You will need to understand the geometric principles relating to triangles.

You will need to know how to apply the Pythagorean theorem, as well as how to calculate perimeter and area.

Problem: The perimeter of the square shown below is 24 units. What is the length of line segment AB?

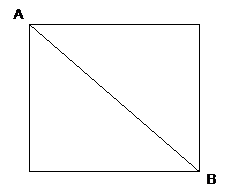
Solution: Remember that the perimeter is the measurement along the outside edges of a geometrical figure.

Since the figure in this problem is a square, we know that the four sides are equal in length.

To find the length of one side, we therefore divide the perimeter by four.

24 ÷ 4 = 6

Now use the Pythagorean theorem to find the length of line segment AB.

Remember the Pythagorean theorem states that the length of the hypotenuse is equal to the square root of the sum of the squares of the two other sides of the triangle.

The hypotenuse is the part of a triangle that is opposite to the right angle.

In this problem, line segment AB is the hypotenuse.

Each side is 6, so the square of each side is 6² = 36.

The sum of the squares of the two sides is 36 + 36 = 72.

The hypotenuse length is the square root of sum of the squares of the two sides, which we have calculated above.

So, the answer is the square root of 72.

Geometry - Rectangles

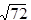
This part of the math section will cover the calculation of the perimeter and area of rectangles.

These types of problems may pose a practical situation, like the one here.

Problem: A farmer wants to put a fence around a small field.

The fence will be constructed with panels, and each panel is 1 yard in length.

The field is rectangular, and its measurements are 14 yards by 10 yards.

How many panels does the farmer need for the entire perimeter of the field?

Solution: Perimeter is the measurement along the outer edges of a square or rectangular area.

If the field is 14 yards by 10 yards, we need 14 yards × 2 to erect the fence on the longer sides of the field.

We need 10 yards × 2 for the other sides of the field.

(14 × 2) + (10 × 2) = 48

So, the farmer needs 48 panels to enclose the field.

Geometry - Circles

You will need to know how to calculate the following concepts relating to circles: diameter, radius, area, circumference, vertices, and arcs.

Problem: If a circle has a radius of 8, what is the circumference of the circle?

Solution: The circumference of a circle is always calculated by using this formula: π times the diameter.

The diameter of a circle is always equal to the radius times 2.

So, the diameter for this circle is 8 × 2 = 16.

Therefore, the circumference is 16π.

Geometry - Three Dimensional Shapes

For three-dimensional shapes, you may need to determine the area of a cone or three-dimensional square, for instance.

Problem: Find the volume of a cone which has a radius of 5 and a height of 6.

Solution: Cone volume = (π × radius² × height) ÷ 3

Now substitute the values for base and height.

volume = (π5² × 6) ÷ 3 =

(π25 × 6) ÷ 3 =

π150 ÷ 3 =

50π