Here are practice problems and solutions for the areas that are covered on the algebra section of the Compass mathematics test.
Basic Algebraic Calculations with Polynomials
Remember that a polynomial is a mathematical equation that contains more than one variable, such as x or y.
Problem: (x + 2y)2 = ?Solution: This type of algebraic expression is known as a polynomial.
To solve this sort of problem, you need the "FOIL" method.
"FOIL" stands for First - Outside - Inside - Last.
So, you have to multiply from the terms from each of the two pairs of parentheses in this order:
(x + 2y)2 = (x + 2y)(x + 2y)
FIRST − Multiply the first term from the first pair of parentheses with the first term from the second pair of parentheses.
x × x = x2
OUTSIDE − Multiply the terms at the outer part of each pair of parentheses.
x × 2y = 2xy
INSIDE − Multiply the terms at the inside, in other words, from the right on the first pair of parentheses and from the left on the second pair of parentheses.
2y × x = 2xy
LAST − Multiply the second terms from each pair of parentheses.
2y × 2y = 4y2
Then we add all of the above parts together for the final answer.
x2 + 2xy + 2xy + 4y2 =
x2 + 4xy + 4y2
Factoring Polynomials and Other Algebraic Expressions
"Factoring" means that you need to break down the equations into smaller parts.
Problem: Factor the following algebraic expression.
x2 + x − 30
Solution: For any problem like this, the answer will be in the following format: (x + ?)(x − ?)
We know that we need to have a plus sign in one pair of parentheses and a minus sign in the other pair of parentheses because 30 is negative.
We can get a negative number in problems like this only if we multiply a negative and a positive.
We also know that the factors of 30 need to be one number different than each other because the middle term is x, in other words 1x.
The only factors of 30 that meet this criterion are 5 and 6.
Therefore the answer is (x + 6)(x − 5)
Substituting Values into Algebraic Equations
You will see an equation with x and y, and you will have to replace x and y with the values stipulated in the problem.
Problem: What is the value of the expression 2x2 − xy + y2 when x = 4 and y = −1 ?
Solution: To solve this problem, put in the values for x and y and multiply.
Remember to be careful when multiplying negative numbers.
2x2 − xy + y2 =
(2 × 42) − (4 × −1) + (−12) =
(2 × 4 × 4) − (−4) + 1 =
(2 × 16) + 4 + 1 =
32 + 4 + 1 =
37
Algebraic Equations for Practical Problems
These types of problems are expressed in a narrative format. They present a real-life situation.
For instance, you may be asked to create and solve an equation that can be used to determine the discount given on a sale.
Problem: Sarah bought a pair of jeans on sale for $35. The original price of the jeans was $50.
What was the percentage of the discount on the sale?
Solution: To determine the value of a discount, you have to calculate how much the item was marked down: $50 − $35 = $15
Then divide the markdown by the original price: 15 ÷ 50 = 0.30
Finally, convert the decimal to a percentage: 0.30 = 30%
Coordinate Geometry
This aspect of geometry is included on the algebra part of the test because you need to use algebraic concepts in order to solve these types of geometry problems.
Coordinate geometry problems normally consist of linear equations with one or two variables.
You may need to calculate geometric concepts like slope, midpoints, distance, or x and y intercepts.
Problem: State the x and y intercepts that fall on the straight line represented by the following equation.
y = x + 3
Solution: First you should substitute 0 for x.
y = x + 3
y = 0 + 3
y = 3
Therefore, the y intercept is (0, 3).
Then substitute 0 for y.
y = x + 3
0 = x + 3
0 − 3 = x + 3 − 3
−3 = x
So, the x intercept is (−3, 0).
Rational Expressions with Exponents and Radicals
These types of algebra questions consist of equations that have exponents or square roots or both.
Problem: What is the value of b?
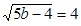
Solution: Your first step is to square each side of the equation.
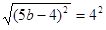
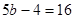
Then get the integers on to just one side of the equation.
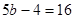
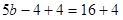
5b = 20
Then isolate the variable b order to solve the problem.
5b ÷ 5 = 20 ÷ 5
b = 4
Now have a look at our other practice test material:
